Pitons rassurants, cordelette pimpante, relais béton ? Attention ! Pour relier deux points, il faut prendre en considération les forces qui s’exercent sur chacun d’eux. A défaut, le résultat pourrait bien être très dangereux. Petit rappel de ce qu’il faut faire et ne pas faire.
Mon ami Sébastien Laurent, grand guide de montagne devant l’éternel, à gravi l’arête des Débrouillards, dans le massif des Trois Becs, dernièrement.
Cette course d’arête au caractère alpin mais à l’engagement et à la difficulté modérée, se termine par un rappel de 50 mètres permettant d’échapper à un final dans de raides pentes d’herbe.
Quelle ne fut pas sa surprise de tomber sur ce relais.
©Sébastien Laurent
Oui ce relais n’est pas optimum. Tous le monde, connait le concept de projection géométrique des force (cours de physique de seconde ?).
Celui-là même qui explique la tension forte des câbles du téléphérique sur ses deux amarrages, malgré un poids relativement faible de la cabine. Et que dans l’absolu, la projection d’une force à 90° est multipliée par un facteur qui est infini. D’où la flèche nécessaire des câbles du déjà cité téléphérique.
Pour notre pratique alpine, je vous ai trouvé un petit schéma qui explique le problème dans le cas du relais de rappel qui nous intéresse.
La force que représente le poids d’un objet = Poids (en kg) X g (la gravité en N/kg) = P X 9, 81 (résultat en newton (N).
Dans notre cas : 50 kg X 9,81 = 490 N
Dans une première approche grossière, on pourrait croire que la force générée par le poids du grimpeur se partage en deux sur chaque amarrage. Soit 490 N / 2 = 245 N par point.
Hors, suivant les lois de la physique et la fameuse projection géométrique des forces, nous voyons sur le schéma ci-dessus qu’il faut descendre sous un angle de 40° formé par la sangle pour diviser la force générée par le poids du grimpeur par deux.
Et que dès que l’angle augmente, les efforts sur les points ne sont plus partagés,. Pire, ils vont rapidement (aux alentours de 120°) dépasser la force générée par le poids du grimpeur sur chacun des points. Pour finir pour un angle plat ( 180°) de la sangle d’amarrage par une projection d’une force théorique (oui, uniquement théorique car un lien souple ne reste pas à 180° sous une tension perpendiculaire) infinie sur chacun des ancrages.
Nous voyons sur la photos ci-dessus que la cordelette rouge fait un angle d’environ 90°, soit une augmentation de 40% environ par rapport une répartition parfaite (qui divise par deux). Mais il y a pire !
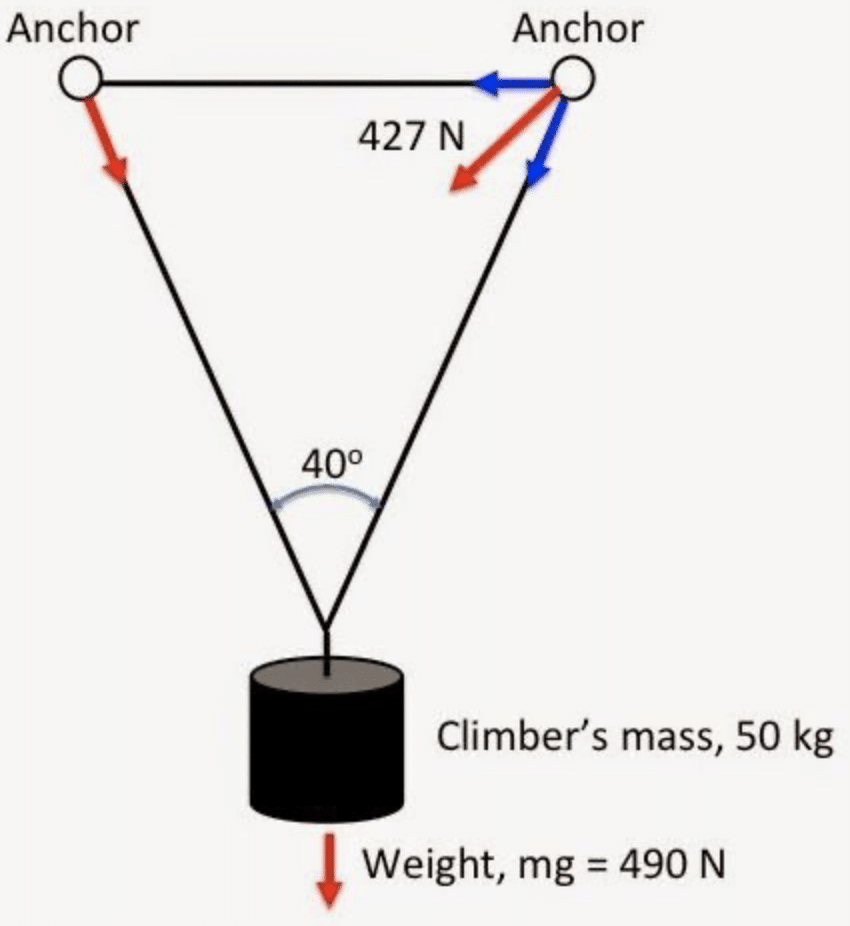
Le fameux triangle de la mort, nommé ainsi par les grimpeurs américains (American Death Triangle).
Dans ce schéma, nous pouvons voir que le fait de passer la sangle en triangle, et non en V, amène des efforts supplémentaires sur chacun des points.
Schéma N° 1. Le poids de 50 kg du grimpeur exerce une force de 490 N et qui partagée sur deux points avec une sangle en V, offrant un angle de 40°: l’effort sur chaque point est de 261 N
Schéma N° 2. Ici, avec le même grimpeur et le même angle mais la sangle posée en triangle, nous obtenons une force de 427 N sur chaque point soit une augmentation d’environ 63% !
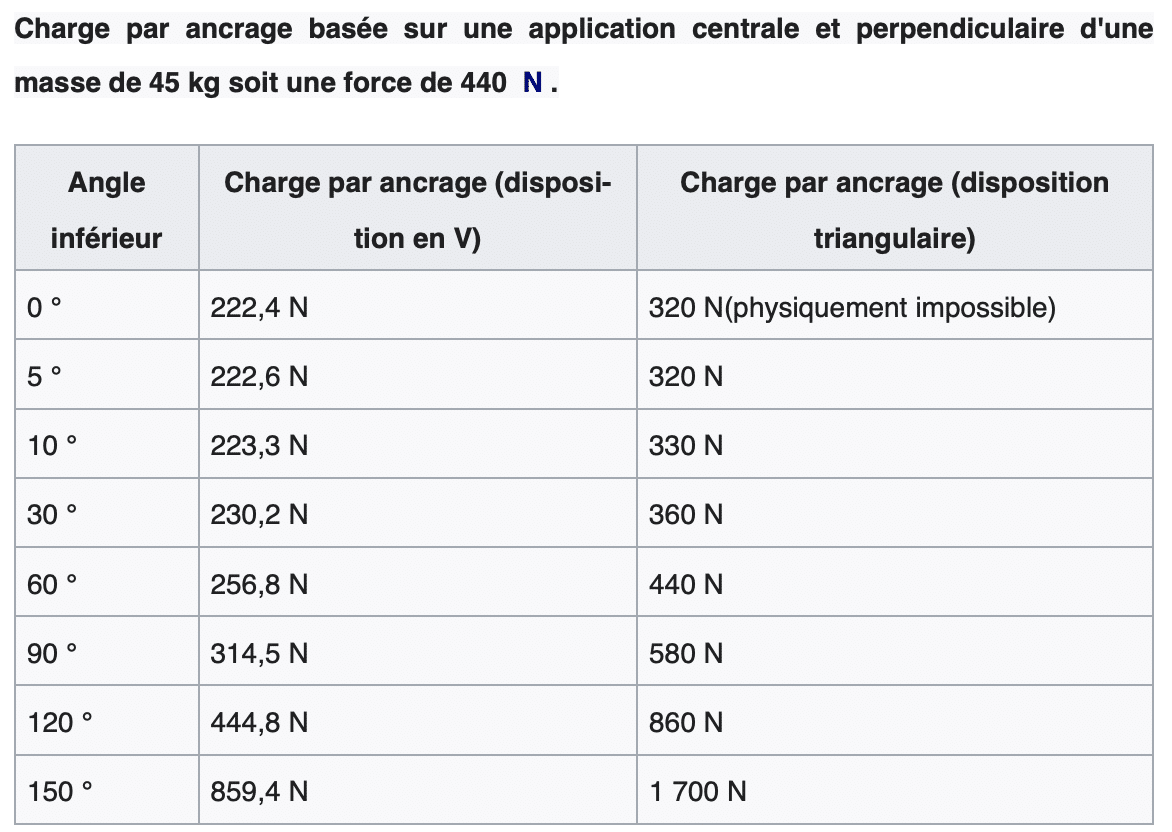
Je vous laisse imaginer (ou calculer ou encore regarder le tableau ci-dessous) la force générée dans le cas de ce relais qui multiplie les erreurs : angle de 90 ° + pose en triangle de la mort !
Source : Wikipédia
Sébastien connaissant sa physique alpine sur le bout des doigts, ne pouvait pas, pour lui et la communauté grimpantes laisser un tel mauvais exemple perdurer. Il a donc modifié le placement de la cordelette pour transformer ce triangle de la mort en un relais en V, avec un angle inférieur à 90°.
Merci à lui !
Le relais modifié. ©Sébastien Laurent
